The newly introduced BBND feature of Netgen/NGSolve allows us to compute the magnetic field of a thin wire by approximating it with operators on the 1D line segment. In this example we want to compute the field of the following coil geometry:
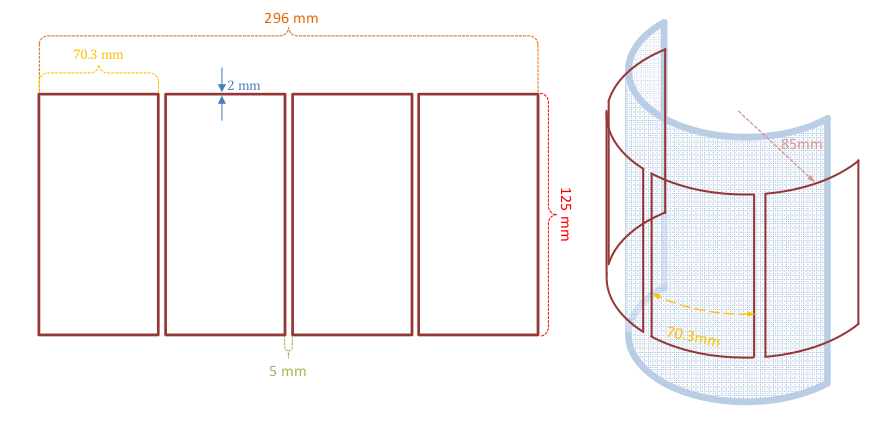
To see how this geometry is constructed using Netgen, have a look at BBND - A New Feature of Netgen 6.2, the file createCoil.py is attached again. This SplineGeometry is then added to a CSGeometry containing an enclosing Sphere.
geo = CSGeometry() geo.Add(Sphere(Pnt(0,0,0),0.3).bc("outer").mat("air")) surfaces = CreateCyl([0,0,0],[0,0,1],[0,0.085,0],0.073,0.125,0.01,4,0.005) for surface in surfaces: geo.AddSplineSurface(surface) mesh = Mesh(geo.GenerateMesh(maxh=0.05)) Draw(mesh)
This generates this (pretty raw) mesh:

Note that one could change the meshsize at each surface and/or segment. On this geometry we want to solve the following problem:
Find \(u \in H_{\text{curl}}(\Omega) \) such that $$ \int_{\Omega} \frac{1}{\mu} \text{ curl}(u) \text{ curl}(v) - k^2 \varepsilon u v \hspace{0.1cm} dx + \int_{\Gamma_W} \sigma d k i u_T v_T \hspace{0.1cm} dx - \int_{\partial \Omega} ik \sqrt{\frac{\varepsilon}{\mu}} u_T v_T \hspace{0.1cm} dx = \int_{\Gamma_C} I_s v_T \hspace{0.1cm} dx $$ for all \( v \in H_{\text{curl}}(\Omega) \). Here \(\mu, \varepsilon \) and \(\sigma\) are the usual electromagnetic coefficients, \(d\) is the diameter of the wire, \(i\) the imaginary unit, \(k \) the frequency, \(\Gamma_W\) the BBND lines defined as "wire", \(\Gamma_C\) the BBND lines defined as "contact", \(I_s\) the on the contact imposed current and \(u_T\) and \(v_T\) the respective traces depending on the codimension of the integral. The boundary term on \(\partial \Omega\) is a first order transparent boundary condition, to approximate an open domain.
To implement this we define a HCurl finite element space and the corresponding TrialFunction and TestFunction
fes = HCurl(mesh,order=2,complex=True) u,v = fes.TrialFunction(), fes.TestFunction()
a = BilinearForm(fes) a += SymbolicBFI(1./mu * curl(u) * curl(v) - k*k*eps * u * v) a += SymbolicBFI(sigma * d * k * 1J * u.Trace().Trace() * v.Trace().Trace(), definedon=mesh.BBoundaries("wire")) a += SymbolicBFI(-1J * k * sqrt(eps/mu) * u.Trace() * v.Trace(), definedon=mesh.Boundaries("outer")) f = LinearForm(fes) f += SymbolicLFI(Is * v.Trace().Trace(), definedon=mesh.BBoundaries("contact"))
After defining a GridFunction on the space we only have to assemble everything and solve the system. Then we can draw our solution and the magnetic field.
u = GridFunction(fes,"u") with TaskManager(): a.Assemble() f.Assemble() u.vec.data = a.mat.Inverse() * f.vec Draw(u) Draw(curl(u),mesh,"B")

If you have any questions feel free to leave a comment below!

